文章出處：知識中心 網(wǎng)責(zé)任編輯：洛陽軸承 閱讀量： 發(fā)表時間：2022年03月22日
在磁懸浮轉(zhuǎn)子不平衡振動控制的相關(guān)研究基礎(chǔ)上，闡述了磁懸浮轉(zhuǎn)子不平衡振動的產(chǎn)生原因、控制原理以及處理方法，討論了基于軸承電磁力最小和轉(zhuǎn)子振動位移最小這2種控制策略的不平衡振動控制方法，并介紹了該技術(shù)在旋轉(zhuǎn)機械中的典型應(yīng)用案例，最后展望了磁懸浮轉(zhuǎn)子不平衡振動控制研究的未來方向。
由于設(shè)計和加工缺陷、材質(zhì)不均勻、熱變形等原因使得轉(zhuǎn)子不可避免地存在質(zhì)量不平衡，從而會產(chǎn)生與轉(zhuǎn)速同頻的離心力，該離心力與轉(zhuǎn)子轉(zhuǎn)速平方成正比且使轉(zhuǎn)子產(chǎn)生振動。當(dāng)旋轉(zhuǎn)機械高速運轉(zhuǎn)時，微小的殘余不平衡質(zhì)量也會給系統(tǒng)帶來嚴重影響。據(jù)相關(guān)統(tǒng)計，旋轉(zhuǎn)機械故障中約三分之一來自轉(zhuǎn)子不平衡，因此，轉(zhuǎn)子的動平衡以及不平衡振動控制技術(shù)對于高速旋轉(zhuǎn)機械具有非常重大的意義。
傳統(tǒng)結(jié)構(gòu)軸承作為支承時不具備主動控制特性，由其支承的轉(zhuǎn)子只能在實際運行前進行離線動平衡，而且轉(zhuǎn)子經(jīng)過動平衡后仍存在殘余不平衡量，當(dāng)轉(zhuǎn)子因負載變化或生銹等原因?qū)е虏黄胶馇闆r發(fā)生改變時，動平衡將失效。磁軸承的剛度相對于傳統(tǒng)結(jié)構(gòu)軸承較小且懸浮氣隙較大，當(dāng)轉(zhuǎn)子不平衡力較大時，轉(zhuǎn)子振動會更加劇烈；但磁軸承控制參數(shù)與控制電流可調(diào)，使其具備實時主動控制能力，為轉(zhuǎn)子的不平衡振動控制提供可能。
本文基于大量文獻調(diào)研，在磁懸浮轉(zhuǎn)子不平衡振動控制發(fā)展、研究現(xiàn)狀、算法分類等方面展開討論，并提出了未來可能的研究方向。
1、磁懸浮轉(zhuǎn)子系統(tǒng)簡介
磁懸浮柔性轉(zhuǎn)子系統(tǒng)是典型的機電一體化系統(tǒng)，包括控制器、D/A轉(zhuǎn)換模塊、功率放大器、轉(zhuǎn)子、定子、電渦流位移傳感器和A/D轉(zhuǎn)換模塊，典型的磁懸浮轉(zhuǎn)子系統(tǒng)結(jié)構(gòu)如圖1所示。磁懸浮轉(zhuǎn)子的閉環(huán)控制系統(tǒng)原理如圖2所示：電渦流位移傳感器檢測轉(zhuǎn)子相對于參考位置r的偏移e，經(jīng)A/D轉(zhuǎn)換后作為數(shù)字量輸入到控制器，控制器經(jīng)過相應(yīng)的控制算法運算輸出控制信號u，經(jīng) D/A轉(zhuǎn)換后輸入到功率放大器，功率放大器產(chǎn)生控制電流i并使轉(zhuǎn)子穩(wěn)定在平衡位置。
1—非驅(qū)動端徑向磁軸承；2—激勵磁軸承；3—盤片；4—轉(zhuǎn)軸；5—驅(qū)動端徑向磁軸承；6—電動機；7—位移傳感器。
圖1 典型的磁懸浮轉(zhuǎn)子系統(tǒng)結(jié)構(gòu)
Fig.1 Typical magnetic suspension rotor system structure
圖2磁懸浮轉(zhuǎn)子控制系統(tǒng)原理圖
Fig.2Principle of magnetic suspension rotor control system
2、磁懸浮轉(zhuǎn)子不平衡控制方法
目前，磁懸浮轉(zhuǎn)子不平衡振動控制策略有軸承電磁力最小控制和轉(zhuǎn)子位移最小控制這2種。
軸承電磁力最小控制也稱為自動平衡(Auto Balance)，即通過一定的濾波算法將反饋位移信號中的不平衡量濾除，降低控制電流中不平衡同頻分量的幅值以減弱磁軸承的主動控制作用，從而使轉(zhuǎn)子盡可能地繞其慣性主軸轉(zhuǎn)動，此時轉(zhuǎn)子的不平衡控制力最小。通過對轉(zhuǎn)子的不平衡力進行控制，可以使其自由地繞慣性主軸旋轉(zhuǎn)，減小不平衡力的同時消除傳遞至支承基礎(chǔ)的同頻振動力。有效利用不平衡力控制算法減小轉(zhuǎn)子的同頻振動力，對提高磁軸承系統(tǒng)性能及可靠性，降低磁軸承功耗等均有重要意義。
轉(zhuǎn)子位移最小控制也稱為不平衡補償(Unbalance Compensation)，即通過一定措施或補償算法增大控制電流，從而增強磁軸承的主動控制作用，增加系統(tǒng)動剛度，使轉(zhuǎn)子盡可能繞其磁軸承定子的幾何中心轉(zhuǎn)動，以實現(xiàn)減小轉(zhuǎn)子位移振動的目的，此時轉(zhuǎn)子振動位移最小。利用不平衡位移控制算法減小轉(zhuǎn)子的不平衡位移，對增加磁軸承動態(tài)剛度，提高系統(tǒng)輸出精度等具有重要意義。
上述2種振動補償所實現(xiàn)的目的和達到的效果相反，也就是說在主動磁軸承系統(tǒng)中不能同時實現(xiàn)慣性力最小和位移最小。如圖3所示，2種不平衡控制策略的區(qū)別在于虛線框中的不平衡濾波器或補償器在磁懸浮轉(zhuǎn)子控制框圖中的位置，2種控制策略分別在控制器前、后引入控制，事實上針對2種控制策略所設(shè)計的控制算法大多也是在虛線框內(nèi)進行。
圖3 磁懸浮轉(zhuǎn)子不平衡控制原理
Fig.3 Schematic diagram of unbalanced control for magnetic suspension rotor
2.1 軸承電磁力最小控制
按照抑制分量的不同，軸承電磁力最小控制方法可以分為2種：1)同頻力抑制，只抑制轉(zhuǎn)子不平衡帶來的振動力；2)諧波力抑制，在抑制轉(zhuǎn)子不平衡帶來的振動力的同時，還抑制傳感器諧波噪聲等帶來的諧波振動力。
2.1.1 同頻振動抑制
同頻振動抑制又有2種途徑，一種是直接去除同頻量或諧波成分，另一種是識別不平衡量后主動改變控制量。
對于直接去除同頻量或諧波成分的途徑，主要有廣義陷波器、最小均方( Least Mean Square，LMS)算法等。廣義陷波器由于結(jié)構(gòu)簡單而得到了廣泛研究，1996年，文獻[9]提出了一種結(jié)構(gòu)如圖4所示的廣義多變量陷波器抑制不平衡振動，其在通用陷波器中插入了一個靈敏度調(diào)節(jié)矩陣T以調(diào)整系統(tǒng)極點的位置，從而保證系統(tǒng)的穩(wěn)定性。文獻[10]提出了基于相移通用陷波反饋控制的同頻電流抑制方法，可有效抑制控制器、功放系統(tǒng)和感應(yīng)電動勢產(chǎn)生的同頻電流。為了同時對電流剛度和位移剛度進行補償，文獻[11]提出了將滑模觀測器和陷波器結(jié)合的方法抑制不平衡振動，而且無需區(qū)分電流剛度和位移剛度，也無需考慮功放的低通特性。文獻[12]針對主被動磁懸浮轉(zhuǎn)子的質(zhì)量不平衡以及被動磁軸承中心偏移導(dǎo)致的同頻振動力，提出了一種基于位移陷波加前饋補償?shù)淖詣悠胶饪刂品椒ā?/span>
圖4 基于廣義陷波器的不平衡振動抑制
Fig.4 Unbalanced vibration suppression based on generalized notch filter
20世紀80年代，自適應(yīng)濾波算法獲得蓬勃發(fā)展，起初在噪聲消除方面應(yīng)用廣泛。LMS算法由于原理簡單，自適應(yīng)、抗干擾能力強，收斂性好等優(yōu)點獲得了廣泛應(yīng)用，并于20世紀90年代應(yīng)用于磁懸浮轉(zhuǎn)子不平衡振動控制領(lǐng)域。LMS算法實際上是一種離散自適應(yīng)陷波器，其原理如圖5所示。文獻[14]在2009年提出了基于LMS算法的實時變頻切換控制策略，降低了周期性不平衡激振力；隨后，為兼顧穩(wěn)定性和收斂速度，提出了變步長LMS算法并在不同定轉(zhuǎn)速試驗中取得了較好效果，而將H∞算法與自適應(yīng)步長LMS算法相結(jié)合實現(xiàn)實時最小慣性力補償，則提高了整個系統(tǒng)的魯棒穩(wěn)定性和抗干擾性能。另外，文獻[17]提出了一種基于LMS算法的自適應(yīng)前饋補償，抵消了功放低通特性的影響，其方法原理如圖6所示。
圖5 LMS算法原理
Fig.5 Principle of LMS algorithm
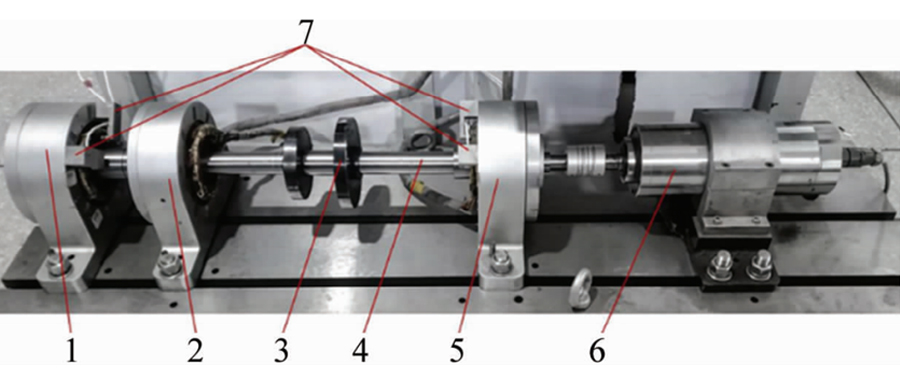
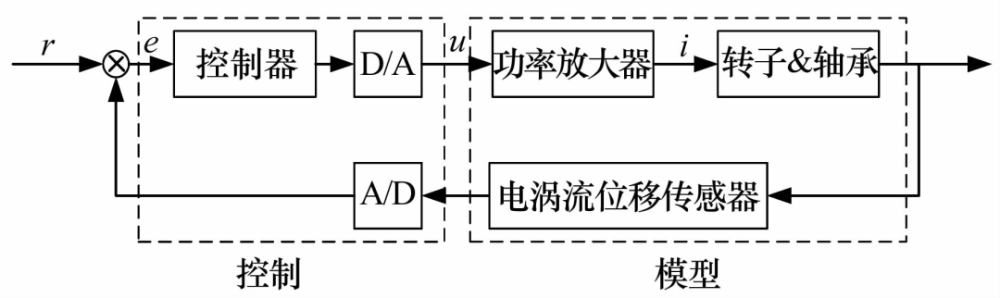
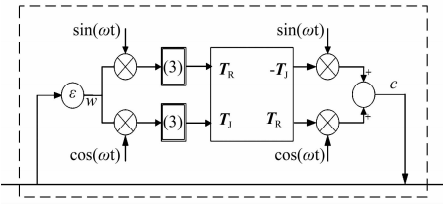
2015年，文獻[18]將電動機傳動控制中同步旋轉(zhuǎn)坐標系(Synchronous Rotating Frame，SRF)變換的方法應(yīng)用于磁軸承系統(tǒng)，其控制原理如圖7所示，相當(dāng)于一種新型的陷波濾波器，通過與控制器串聯(lián)工作在轉(zhuǎn)子低速旋轉(zhuǎn)時有良好的同步抑振性能。
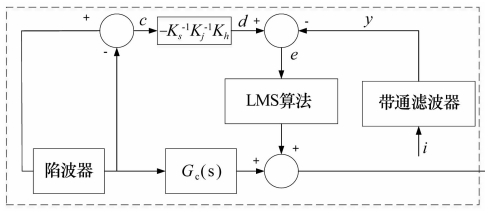
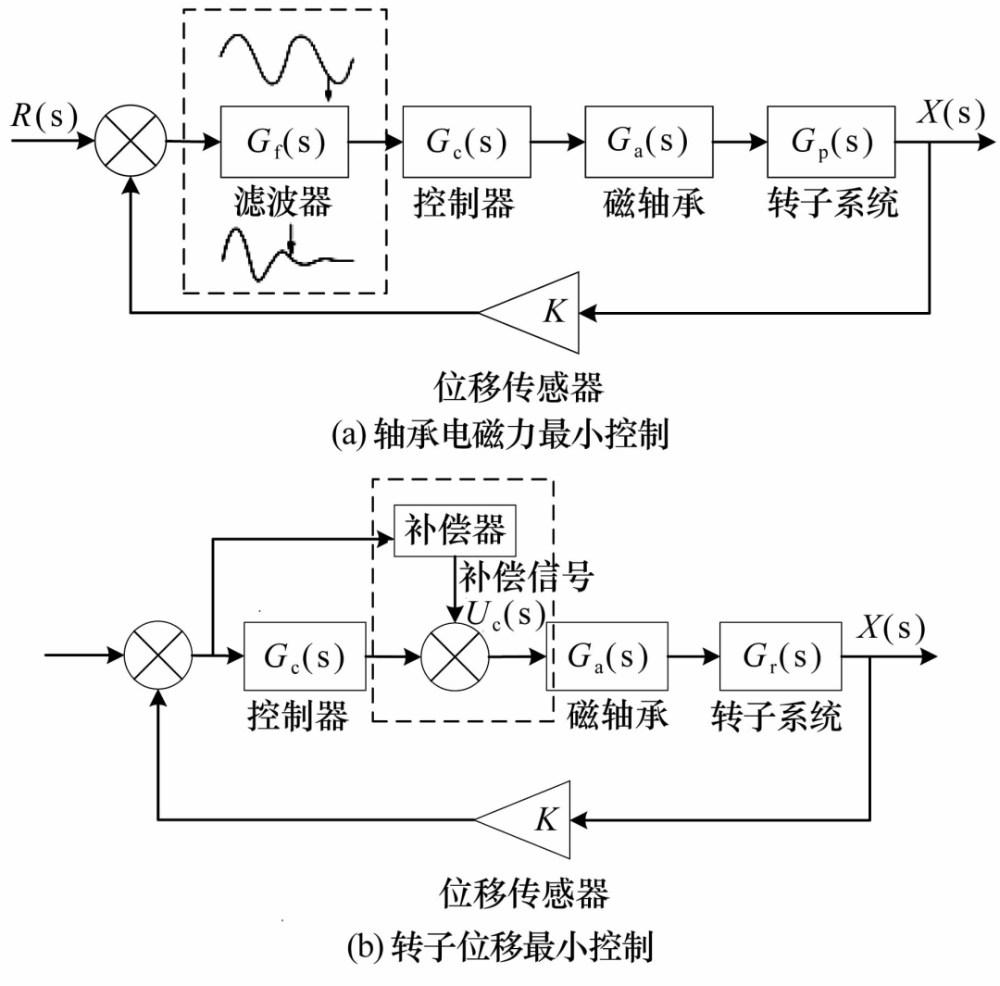
圖6 帶比例前饋補償?shù)淖詣悠胶夥椒?/span>
Fig.6 Automatic balancing method with proportional feedforward compensation
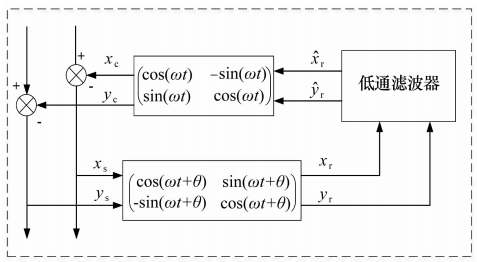
圖7 基于SRF變換的控制原理圖
Fig.7 Control schematic diagram based on SRF
對于識別不平衡量后主動改變控制量的途徑，文獻[19]設(shè)計了自適應(yīng)自平衡控制策略，通過識別慣性軸與幾何軸的位移和夾角進行補償；文獻[20]設(shè)計了滑模擾動觀測器對不平衡力和不平衡力矩進行觀測并補償，有效減小了同頻振動。
2.1.2 諧波振動抑制
諧波振動抑制方法也可分為2種途徑，一種是利用多個濾波器分別抑制各次諧波，另一種是設(shè)計自適應(yīng)算法統(tǒng)一抑制。
對于分別抑制各次諧波的途徑，最典型的就是采用多個陷波器：文獻[21]將多個相移陷波器并聯(lián)實現(xiàn)了可變轉(zhuǎn)速下的電流諧波抑制；文獻[22]進一步給并聯(lián)的多個陷波器分配了不同的相移角，實現(xiàn)了全轉(zhuǎn)速的振動控制；文獻[23]將多個準諧振控制器并聯(lián)并引入阻尼因子，實現(xiàn)了穩(wěn)定性與動態(tài)性能之間的良好平衡；文獻[24]則將多個陷波器串聯(lián)，同樣實現(xiàn)了諧波振動的抑制。
對于統(tǒng)一抑制的途徑，文獻[25]提出了一種非線性自適應(yīng)方法估計諧波干擾的各傅里葉級數(shù)，可以精確補償位移剛度，其控制原理如圖8所示，在低轉(zhuǎn)速下取得了較好的振動抑制效果。
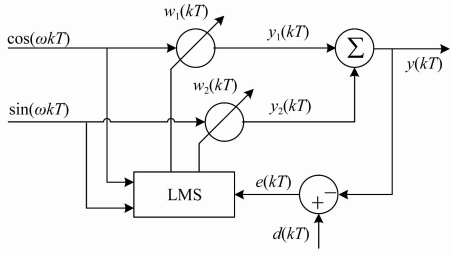
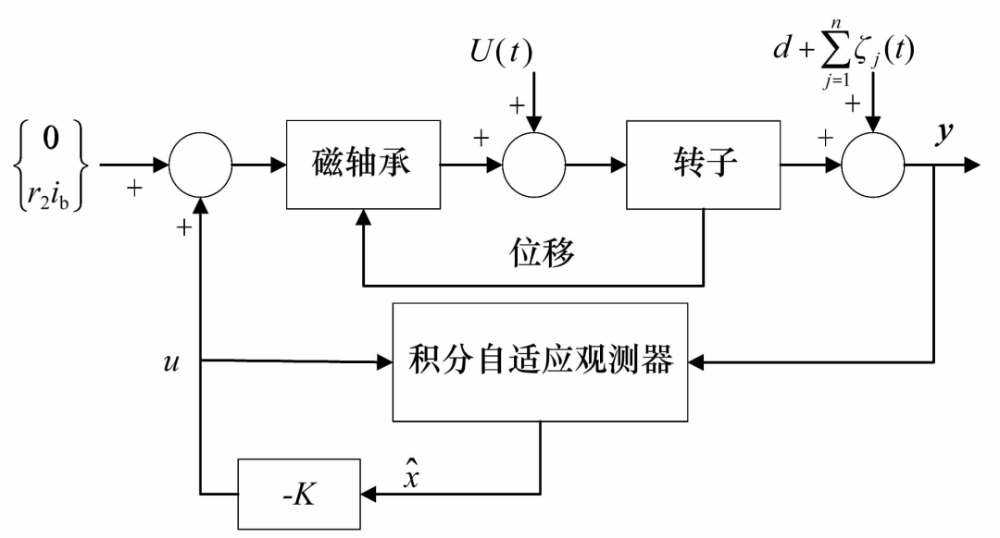
另外，文獻[26]提出了一種基于頻域自適應(yīng)LMS算法的諧波振動抑制方法，對每個權(quán)值設(shè)置相應(yīng)的步長并實時調(diào)整，在保證穩(wěn)態(tài)精度的同時提高了收斂速度。文獻[27]提出了一種新的積分自適應(yīng)觀測器(圖9)，用于識別傳感器誤差的直流和諧波含量并同時估計系統(tǒng)狀態(tài)，試驗表明當(dāng)系統(tǒng)同時受到測量誤差和不平衡干擾時能有效減小位移和電流幅值。文獻[28]提出了一種針對低次主導(dǎo)諧波的通用選擇分數(shù)階重復(fù)控制方法，實現(xiàn)了任意轉(zhuǎn)速下快速高精度的諧波電流抑制。
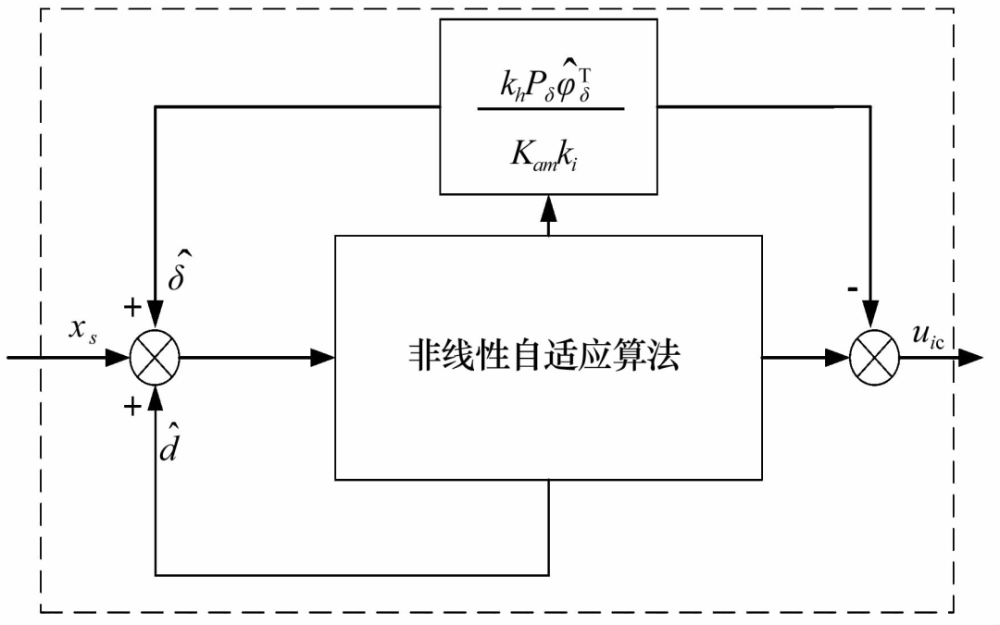
圖8 非線性自適應(yīng)諧波振動控制框圖
Fig.8 Block diagram of nonlinear adaptive harmonic vibration control
圖9 基于積分自適應(yīng)觀測器的諧波振動抑制
Fig.9 Harmonic vibration suppression based on
integral adaptive observer
2.2 轉(zhuǎn)子位移最小控制
相對于軸承電磁力最小控制而言，轉(zhuǎn)子位移最小控制的復(fù)雜度較高，主要體現(xiàn)在實際系統(tǒng)不平衡力的大小和相位難以估計。不平衡力與轉(zhuǎn)子轉(zhuǎn)速ω、不平衡質(zhì)量m 、偏心距e等參數(shù)有關(guān)，可表示為F(t)=meω2sin(ωt+φ)，由于轉(zhuǎn)子轉(zhuǎn)速ω通常已知，如何得到不平衡力的幅值meω2和相位φ成為最小位移補償至關(guān)重要的部分。
2.2.1 轉(zhuǎn)子不平衡補償幅值估計
對于轉(zhuǎn)子不平衡補償信號的幅值估計，目前常用的算法有迭代算法、影響系數(shù)法以及基于模型辨識的方法等。
1983年，文獻[29]最早開始磁懸浮轉(zhuǎn)子不平衡振動控制研究，利用最小二乘法建立磁軸承系統(tǒng)響應(yīng)與控制量之間的聯(lián)系，獲取影響系數(shù)矩陣，利用磁軸承作為不平衡振動控制作動器，采用開環(huán)前饋的方法抑制振動。其基本原理為
y=T(ω)u+d，
式中：y為系統(tǒng)位移響應(yīng)同頻傅里葉系數(shù)；T為影響系數(shù)矩陣；u為不平衡控制同頻傅里葉系數(shù)；d為不平衡力同頻傅里葉系數(shù)。理論上，只需得到各轉(zhuǎn)速下轉(zhuǎn)子不平衡力的分布以及對應(yīng)的影響系數(shù)矩陣，即可計算對應(yīng)轉(zhuǎn)速下所需控制量。但此方法必須要先獲得轉(zhuǎn)子當(dāng)前轉(zhuǎn)速信息及不平衡激振力分布等先驗信息，對影響系數(shù)矩陣的精度有比較高的要求。
文獻[31]提出一種剛性軸不平衡抑制方法，基于之前的磁懸浮轉(zhuǎn)子模態(tài)研究，通過如圖10所示的全息譜方法對轉(zhuǎn)子初始不平衡進行分析，將力不平衡與力偶不平衡分離研究，通過一階、二階振型獲得不平衡相位、增益信息，然后施加反相電磁力抑制轉(zhuǎn)子不平衡。文獻[32]提出一種同時估計動態(tài)參數(shù)和不平衡量的辨識算法，該算法主要基于轉(zhuǎn)子的模型，具有較強的魯棒性，算法結(jié)果與試驗過程中磁軸承轉(zhuǎn)子的動態(tài)參數(shù)一致?；谀Ｐ偷目刂扑惴m然能夠獲得較好的振動控制效果，但獲取精確不平衡力模型的難度較高，且控制效果依賴于模型的精確度。
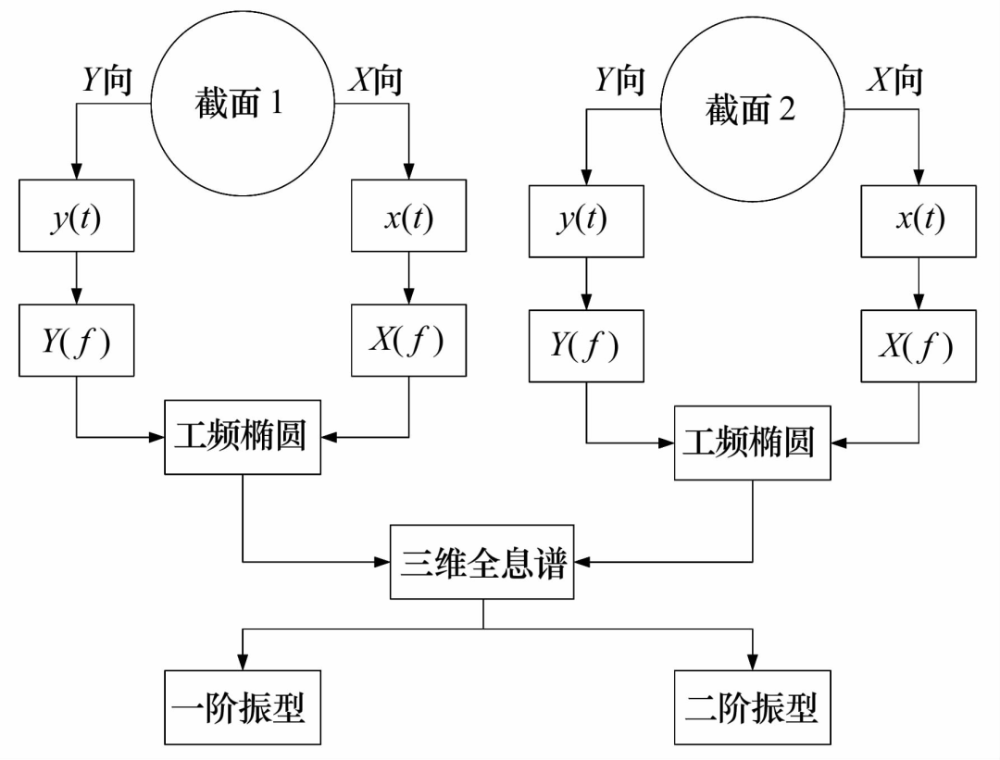
圖10 磁懸浮轉(zhuǎn)子全息譜原理
Fig.10 Holographic spectrum principle of magnetic suspension rotor
為避免過于依賴模型精確度的問題，通過自適應(yīng)算法得到不平衡幅值估計。文獻[33]提出一種基于擴展影響系數(shù)法的磁軸承轉(zhuǎn)子位移跳動檢測方法，解決了之前補償算法中需要對傳感器進行3點設(shè)置以及補償失效的問題，能夠自適應(yīng)識別并補償轉(zhuǎn)子跳動。文獻[34]對影響系數(shù)法進行優(yōu)化，提出了一種廣義影響系數(shù)法并針對不平衡幅值進行了測試，在每次試加質(zhì)量后判斷是否能夠平衡，通過反復(fù)試加以找到最優(yōu)解，在磁懸浮轉(zhuǎn)子高轉(zhuǎn)速工況下能夠得到比傳統(tǒng)影響系數(shù)法更準確的結(jié)果。文獻[35]則提出了一種基于主動磁軸承的影響系數(shù)法，通過主動磁軸承對轉(zhuǎn)子校正面各試加一次與位移同頻同相電流，代替了傳統(tǒng)動平衡的配重與去重，其補償方法如圖11所示，通過計算得到轉(zhuǎn)子不平衡振動補償電流，從而實現(xiàn)轉(zhuǎn)子正常運行中的在線不平衡補償。
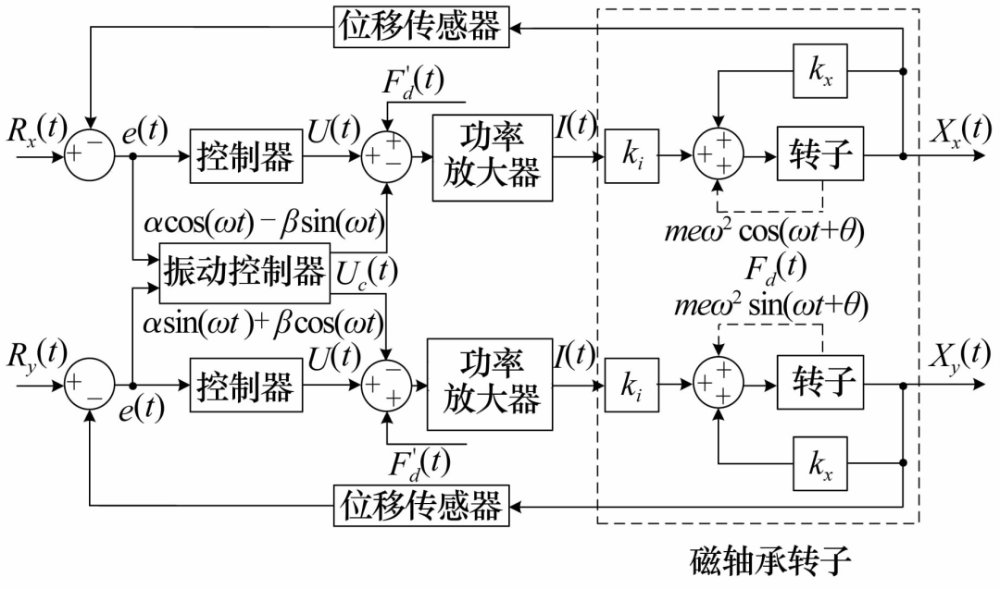
圖11 磁懸浮轉(zhuǎn)子在線動平衡方法
Fig.11 Online dynamic balance method of magnetic suspension rotor
影響系數(shù)法可以在一定程度上看作試加質(zhì)量的反復(fù)迭代求解，對于轉(zhuǎn)子不平衡力的幅值還有另外的方法進行求解。
文獻[36]提出了一種可變步長( Variable Step Size，VSS)的迭代算法，其是對定步長( Constant Step Size，CSS)迭代算法的延伸優(yōu)化，控制方法如圖12所示，通過信號處理模塊、迭代模塊和輸出模塊不斷的迭代計算以找到不平衡力幅值的準確解。2種算法的對比結(jié)果表明，VSS算法具有更好的準確度和收斂速度，當(dāng)轉(zhuǎn)速升高且超過臨界值時CSS算法失去了補償效果，而VSS算法仍可進行補償，能夠更好地抑制轉(zhuǎn)子跨階時的不平衡振動。
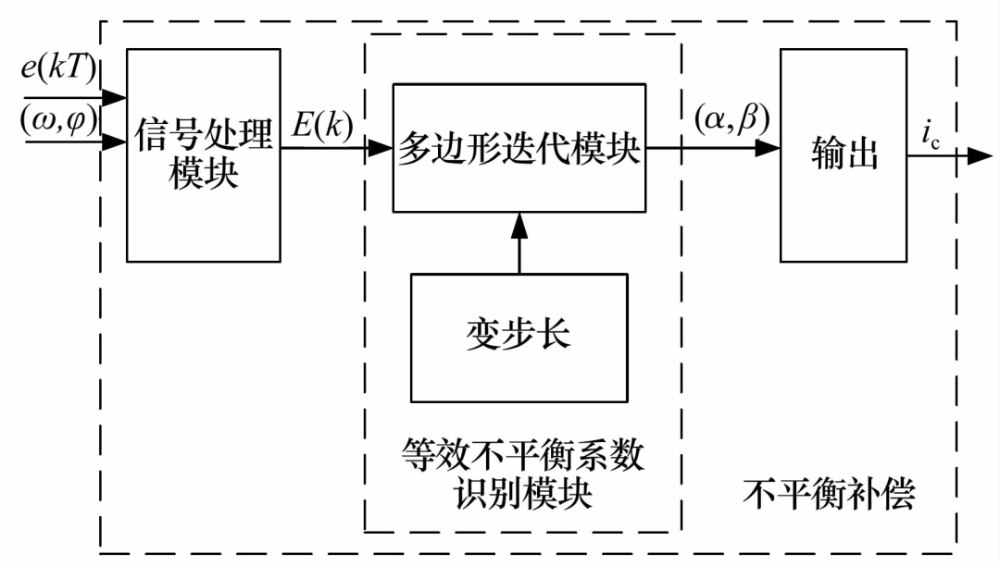
圖12 可變步長迭代算法的不平衡振動控制
Fig.12Variable step size iterative algorithm for unbalanced vibration control
文獻[37]提出了一種尋找不平衡質(zhì)量位置的算法，通過如圖13所示的補償模塊將轉(zhuǎn)子轉(zhuǎn)速作為輸入，根據(jù)實時提取的轉(zhuǎn)子不平衡質(zhì)量的大小和位置產(chǎn)生相應(yīng)的控制信號，從而抑制不平衡振動。由于該不平衡質(zhì)量與轉(zhuǎn)子轉(zhuǎn)速無關(guān)，該算法也適用于變速轉(zhuǎn)子。
圖13 不平衡質(zhì)量尋找算法的振動控制
Fig.13 Unbalanced mass seeking algorithm for vibration control
2.2.2 轉(zhuǎn)子不平衡補償相位估計
轉(zhuǎn)子不平衡補償信號的相位決定了不平衡補償力的方向，理想狀態(tài)下，補償力應(yīng)與不平衡力方向相反大小相等。由于不平衡力作用在磁懸浮轉(zhuǎn)子上使轉(zhuǎn)子產(chǎn)生振動，磁懸浮轉(zhuǎn)子不平衡振動的同頻位移為正弦信號，形如X(t)=Asin(ωt+φ)。因此，現(xiàn)有方法多采用參考信號法估計不平衡補償相位，通過位移傳感器獲取轉(zhuǎn)子實時位移信息，提取由不平衡振動產(chǎn)生的同頻振動位移，以此為參考信號從而獲取相位信息。目前采用較多的算法有LMS算法、陷波器濾波、基于傅里葉系數(shù)的迭代逼近算法，濾波算法等。
文獻[26]提出了一種基于頻域自適應(yīng)的LMS算法，單一通道不平衡振動自適應(yīng)控制框圖如圖14所示，其以諧波振動作為輸入，參考輸入為引入的與傳感器跳動具有相同分量的正弦信號，仿真結(jié)果表明該方法能有效提取磁懸浮轉(zhuǎn)子不平衡同頻振動信號。
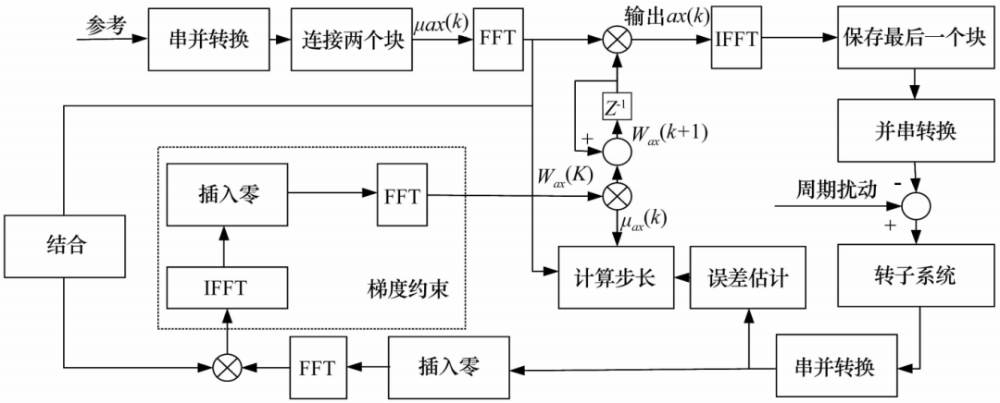
圖14 頻域自適應(yīng)LMS算法
Fig.14 Frequency domain adaptive LMS algorithm
文獻[38]提出了一種基于LMS算法的快速相位追蹤算法，其補償算法框架如圖15所示，將PID和可變步長LMS算法控制策略結(jié)合，在過濾器中補加追蹤算法直到轉(zhuǎn)子速度達到一定值，在DSP架構(gòu)下的實時試驗驗證了該算法的相位跟蹤性能。
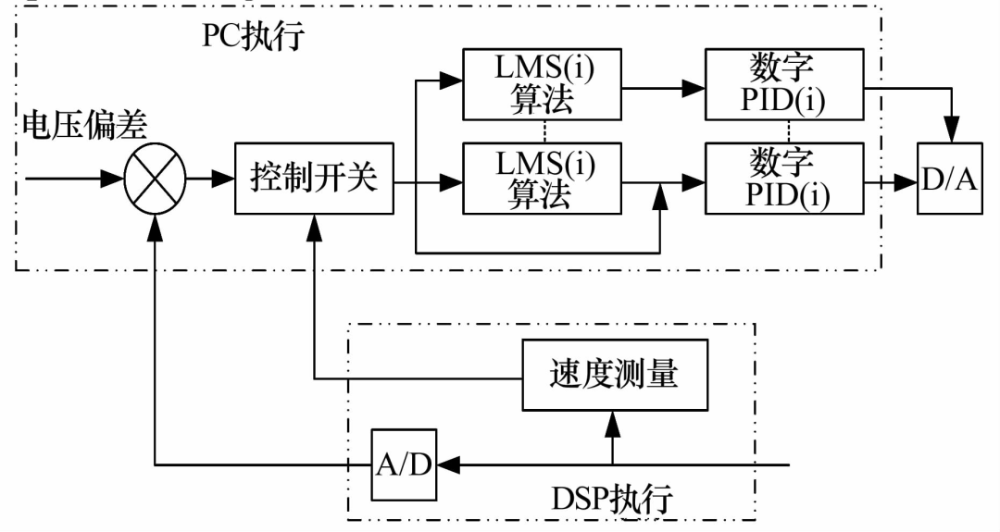
圖15 PID和可變步長LMS算法結(jié)合控制策略
Fig.15 Combined control strategy of PID and variable step size LMS algorithm
LMS算法在轉(zhuǎn)子不平衡補償相位估計中應(yīng)用較多，可以理解為對特定頻率信號的一種陷波算法，除此之外，還有其他的濾波算法用于磁軸承轉(zhuǎn)子不平衡的補償相位估計。文獻[39]利用卡爾曼濾波方法提取不平衡位移量，根據(jù)不平衡位移經(jīng)線性高斯狀態(tài)反饋控制器提高剛度，減小振動。文獻[40]將廣泛應(yīng)用于電動機控制的同步旋轉(zhuǎn)坐標系(SRF)應(yīng)用于磁軸承控制，采用如圖16所示的前饋控制回路，通過單相的位移誤差信號構(gòu)造2路正交信號作為SRF變換的輸入，將同頻位移誤差轉(zhuǎn)變?yōu)橹绷髁?，從而對變換后的直流誤差進行無靜差的跟蹤控制。文獻[41]提出了一種相位補償方法以提高柔性轉(zhuǎn)子在第一彎曲臨界轉(zhuǎn)速附近的阻尼水平，其在控制器中加入相位補償算法使得轉(zhuǎn)子系統(tǒng)整體的阻尼增加，仿真和試驗結(jié)果表明相位補償能夠明顯提高轉(zhuǎn)子的一階彎曲模態(tài)阻尼，有效抑制轉(zhuǎn)子的共振振動，使轉(zhuǎn)子順利通過一階彎曲臨界轉(zhuǎn)速，實現(xiàn)超臨界運行。
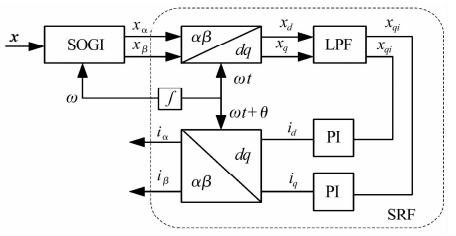
圖16 SOGI-SRF補償器結(jié)構(gòu)圖
Fig.16 Structure diagram of SOGI-SRF compensator
2.3 算法切換控制
軸承電磁力最小算法與轉(zhuǎn)子位移最小算法是2種完全相對的控制方法，各有優(yōu)勢，也各有缺陷。軸承電磁力最小控制算法存在低轉(zhuǎn)速時閉環(huán)系統(tǒng)不穩(wěn)定的問題，轉(zhuǎn)子位移最小算法雖然能夠?qū)崿F(xiàn)轉(zhuǎn)子的高精度旋轉(zhuǎn)，但在高轉(zhuǎn)速工況下容易致使功放飽和且放大轉(zhuǎn)子振動相位與不平衡力的相位差，通常適用于轉(zhuǎn)速較低的情況。對于2種算法的切換控制，有一些學(xué)者展開了研究：文獻[42]利用廣義根軌跡分析了引入補償后系統(tǒng)的閉環(huán)穩(wěn)定性，通過切換引入補償?shù)臉O性穿越臨界轉(zhuǎn)頻，從而實現(xiàn)引入LMS反饋補償后全轉(zhuǎn)速閉環(huán)穩(wěn)定；文獻[43]提出了一種新型多諧振控制器，可在不同轉(zhuǎn)速下實行分段切換策略，實現(xiàn)抑制基波和諧波電流；文獻[44]則提出了基于極性切換陷波器的方法。
2.4 智能控制算法
近年來，在前人研究成果的基礎(chǔ)上，一些新興算法也被提出，如迭代學(xué)習(xí)算法、神經(jīng)網(wǎng)絡(luò)算法等智能算法以及多算法融合控制等。文獻[45]針對磁懸浮轉(zhuǎn)子提出基于學(xué)習(xí)策略的不平衡補償PID控制策略，試驗結(jié)果表明該算法在較大轉(zhuǎn)速范圍內(nèi)的擾動跟蹤效果良好，而通過采用不同的方法進行分析，該文獻認為相對于采用遺忘因子，使用非因果低通濾波器的效果更好。
文獻[46]利用深度學(xué)習(xí)理論設(shè)計了一種補償控制器并將其加入PID反饋控制中，其采用具有2個隱含層的深度神經(jīng)網(wǎng)絡(luò)建立了補償控制器的結(jié)構(gòu)，通過設(shè)計的運行算法仿真了不同控制器在固定轉(zhuǎn)速下的不平衡振動控制，通過不平衡振動分析和控制電流分析驗證了所提控制器的控制效果，但該算法的試驗效果還有待進一步驗證。
3、研究方向與展望
經(jīng)過眾多學(xué)者多年的研究，磁懸浮轉(zhuǎn)子不平衡振動控制領(lǐng)域早已碩果累累，但仍然有以下幾點待開展研究。
3.1 轉(zhuǎn)子跨階時的不平衡補償
當(dāng)轉(zhuǎn)子跨越臨界轉(zhuǎn)速(跨階)時，根據(jù)受迫振動響應(yīng)規(guī)律可知，此時轉(zhuǎn)子的振動幅值與相位都會發(fā)生劇烈變化，且由于轉(zhuǎn)子發(fā)生彎曲形變，轉(zhuǎn)子的不平衡狀態(tài)會發(fā)生改變，現(xiàn)有的算法如自適應(yīng)迭代算法、影響系數(shù)法等可能會失效。而且，目前大多數(shù)研究都是針對剛性轉(zhuǎn)子或跨階后處于穩(wěn)定狀態(tài)的轉(zhuǎn)子。如何設(shè)計控制器，使不平衡補償在轉(zhuǎn)子跨階時也能有效運行，降低轉(zhuǎn)子在跨階時的振動，輔助轉(zhuǎn)子跨越臨界轉(zhuǎn)速，需進一步開展研究。
3.2 基礎(chǔ)激勵等外界干擾時的不平衡振動控制
當(dāng)轉(zhuǎn)子受到如基礎(chǔ)激勵等外界干擾時，由疊加原理可知轉(zhuǎn)子的振動是外界激勵響應(yīng)與不平衡響應(yīng)的疊加，轉(zhuǎn)子的不平衡響應(yīng)可能被外界干擾產(chǎn)生的振動所覆蓋，特別是當(dāng)外界激勵與轉(zhuǎn)速同頻時，轉(zhuǎn)子的不平衡振動信息難以提取，如何提取該狀態(tài)下的轉(zhuǎn)子不平衡振動信息，實現(xiàn)不平衡振動的控制也有待研究。
3.3 磁軸承＋輔助支承時的不平衡振動控制
傳統(tǒng)意義上的磁懸浮轉(zhuǎn)子不平衡補償多是考慮磁軸承單獨支承的情況，對于磁軸承為主要支承，其他支承方式為輔助支承情況下的不平衡振動控制，尚未見相關(guān)研究。例如，近年來興起的磁＋氣混合軸承支承，轉(zhuǎn)子不僅受到電磁力，還受到動壓效應(yīng)產(chǎn)生的氣浮力，轉(zhuǎn)子的不平衡周期振動在受到控制器周期控制力的同時，還受到由于氣隙周期變化產(chǎn)生的周期性波動氣浮力的影響，對于此類支承方式下的轉(zhuǎn)子，首先需要通過研究其動力學(xué)特性獲取轉(zhuǎn)子的不平衡振動特征，然后進行不平衡振動的控制，這一研究仍待開展。
3.4 智能控制算法與現(xiàn)有算法的結(jié)合
智能控制算法在磁軸承上的應(yīng)用還處于起步階段，隨著智能控制理論的進一步發(fā)展，將智能控制引入磁懸浮轉(zhuǎn)子不平衡振動的研究對提高磁懸浮轉(zhuǎn)子性能具有重要意義。目前，這個方向的研究內(nèi)容在于如何結(jié)合現(xiàn)有的控制算法，利用機器學(xué)習(xí)神經(jīng)網(wǎng)絡(luò)等智能算法增強不平衡振動控制算法的自適應(yīng)能力與魯棒性。
4、磁懸浮轉(zhuǎn)子系統(tǒng)簡介
多年來，經(jīng)過國內(nèi)外眾多學(xué)者在磁懸浮轉(zhuǎn)子不平衡振動控制方法上的研究，取得了許多成果，大大拓展了磁軸承在現(xiàn)代工業(yè)技術(shù)、醫(yī)療器械以及航空航天等領(lǐng)域的應(yīng)用范圍。本文針對磁懸浮轉(zhuǎn)子的不平衡振動控制問題，介紹了國內(nèi)外的研究發(fā)展情況，對不同的控制算法進行分類，綜述了部分學(xué)者的研究成果并討論了各方法之間的相同與不同之處，這些成果基于不同的控制算法以及控制策略，針對不同的實際問題，算法間既有相通之處，又有各自的應(yīng)用場合與優(yōu)勢。在實際的應(yīng)用中，如何針對具體的控制對象研究不同的控制方法，以實現(xiàn)期望的效果，仍然是一個巨大的挑戰(zhàn)。
（參考文獻略）
文章發(fā)表于2022年3期《軸承》——磁力軸承專題
軸研所公眾號 軸承雜志社公眾號
Copyright ? 2019 洛陽軸承研究所有限公司, All Rights Reserved 備案號：豫ICP備18028303號-3
營銷熱線
0379-64367521
0379-64880626
13693806700
0379-64886322
0379-64881181
當(dāng)前位置：
返回
